
Secondary active learning resource from Cambridge Mathematics
Active learning is not necessarily about including games into lessons or getting pupils to move around the classroom, although these actions could be involved. Active learning is about students engaging their brains, about them being challenged intellectually, often through promoting discussion, challenging misconceptions and provoking disagreement.
Sometimes this can be achieved by offering questions with multiple potential solutions, some better than others.
This resource was used during a series of workshops run by Cambridge Maths in August in Chennai and Mumbai. It is aimed at secondary pupils who have some understanding of linear, quadratic and possibly cubic graphs. Often these pupils can work with one type of graph but not compare and contrast between each type. They need to recognise the important features of individual graphs, how graphs relate to each other, and what assumptions they are making when working on any mathematical activity.
To begin with, students are given the set of graphs below on a single sheet. They are informed that each graph is drawn on the same set of axis. Their first task is to suggest an equation for each graph and to be ready to justify their choice.
Can you offer an equation for each graph?
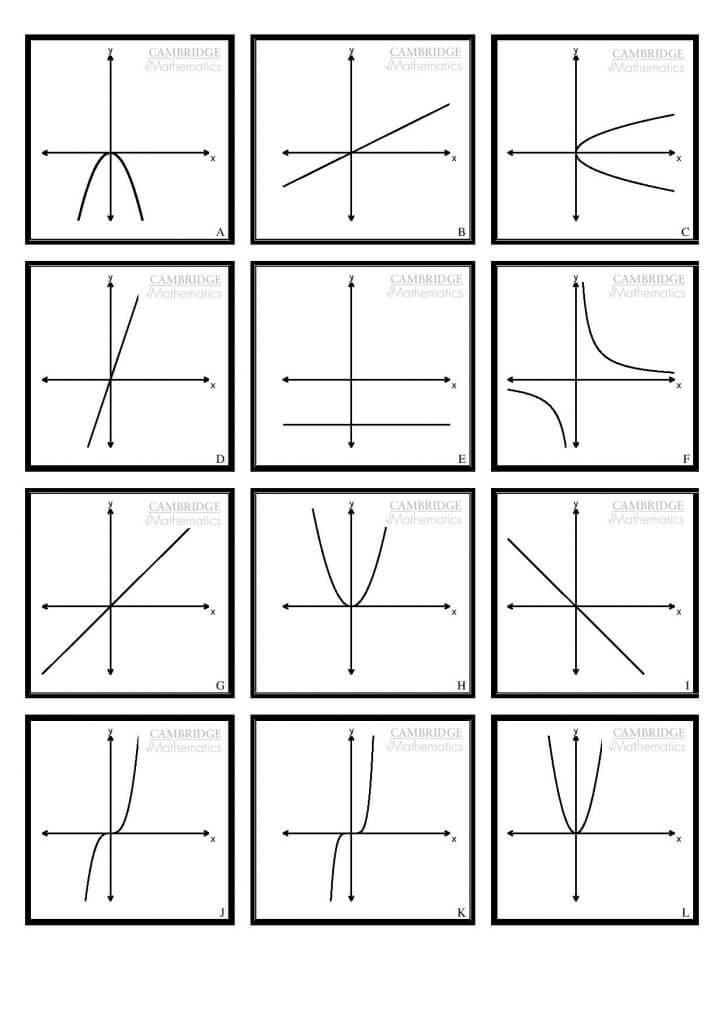
As students complete this first task, the teacher’s job is to go around and probe the ideas being suggested. They should be asking students to explain and justify their given equations, asking about how the graphs are related, and search for any misconceptions that need to be challenged.
Some groups may complete this first task relatively quickly. Asking them to offer alternative solutions, to search for patterns in their solutions and compare with other groups, allows for further development.
Once students have a set of suggestions they are encouraged to share and discuss with other groups.
Rather than go through as a class and discuss each graph in turn students are then offered a set of equations by the class teacher. They should match these up to the graphs, compare to their own ideas and search for any patterns, some may be able to generate general solutions for individual graphs, others may even be able to offer general solutions for graphs and their relations.
Here is the set of offered equations:
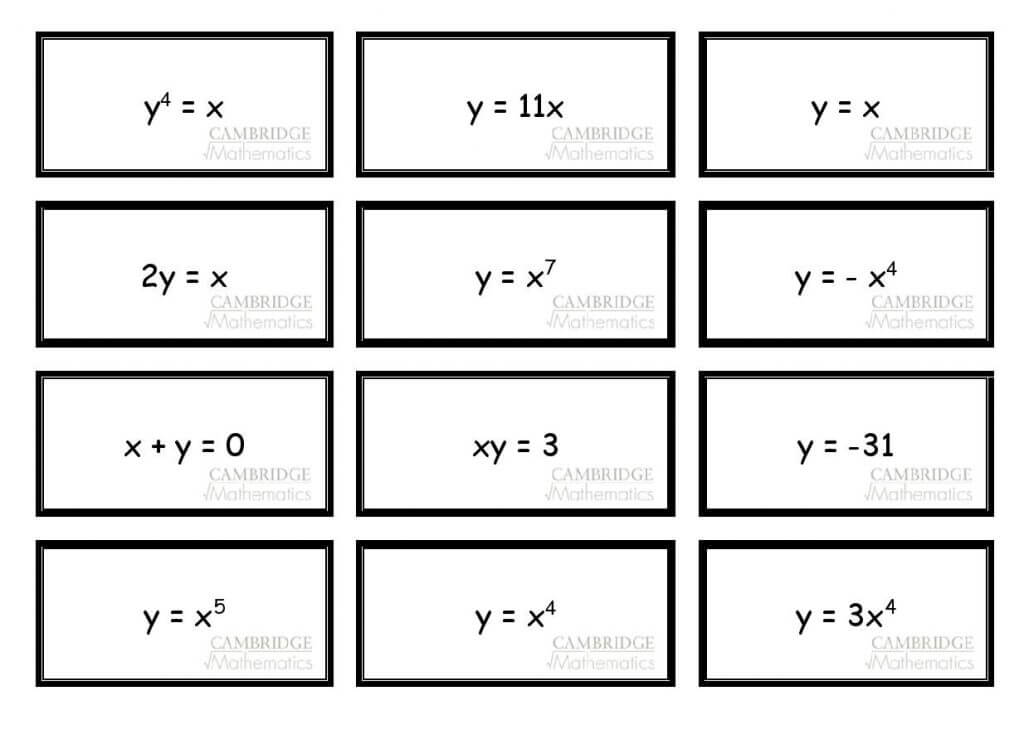
The equations are carefully designed to challenge students’ understandings. They are probably not what you expected. This may cause a bit of cognitive conflict, a hiccup, a moment to pause and ask ‘What is going on?’.
Each equation matches up with a graph, discussions can be encouraged to explain why. These discussions could include why y=x4 looks like a quadratic? Well, it can be re-written y=(x2)2, as can any even power (linking to indices rules), so all even powered quadratics take a similar shape. What about odd powers? Why do they have the shape going from negative into positive? Discussion can center on the effects of repeated multiplication of negative and positive numbers. There are also great opportunities here to look at growth rates of y=x3, y=2x3, y=x5 and y=x7.
In this suggested set of equations, one key assumption has been made. This is demonstrated by the fact that graph G has been identified as y=x. Is this necessarily true? What is the assumption? It takes some thinking about but the assumption is that the graphs axis is in the ratio one-to-one. Can students suggest a set of equations where this assumption is not made?
Finally, I want you to consider how the nature of this task would have changed if the graphs had included scales? How would the approach taken vary? Would the emphasis of discussions change?
About Cambridge Mathematics
Cambridge Mathematics is an organisation rethinking support for curriculum design in mathematics. We are developing a flexible and interconnected digital Framework to help reimagine mathematics education 3-19. Our design process is transparent, collaborative and research- and evidence-informed.




